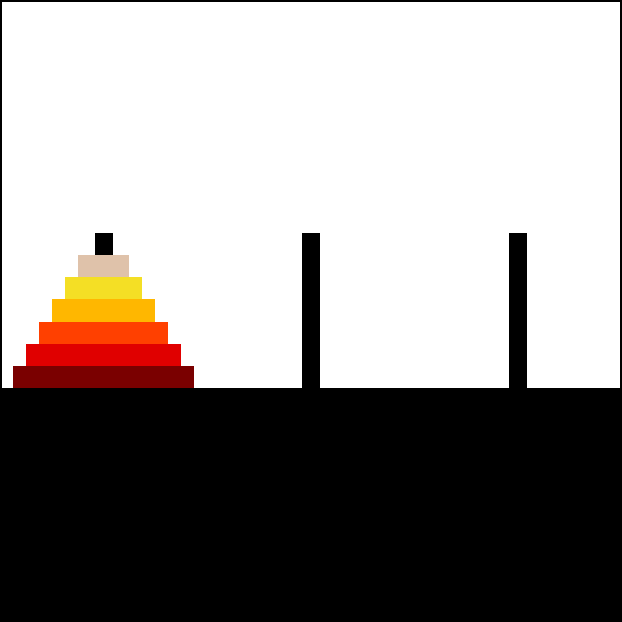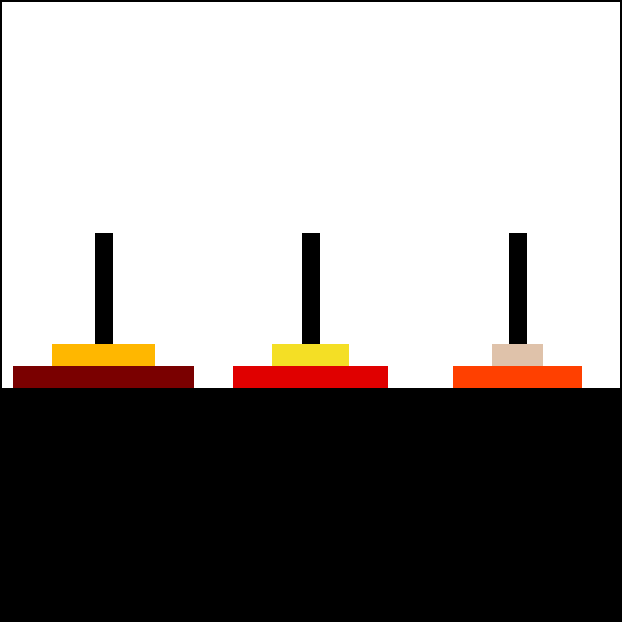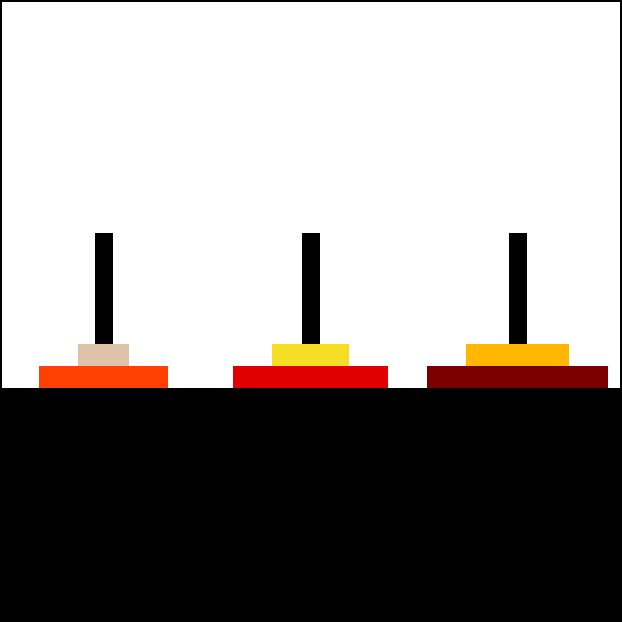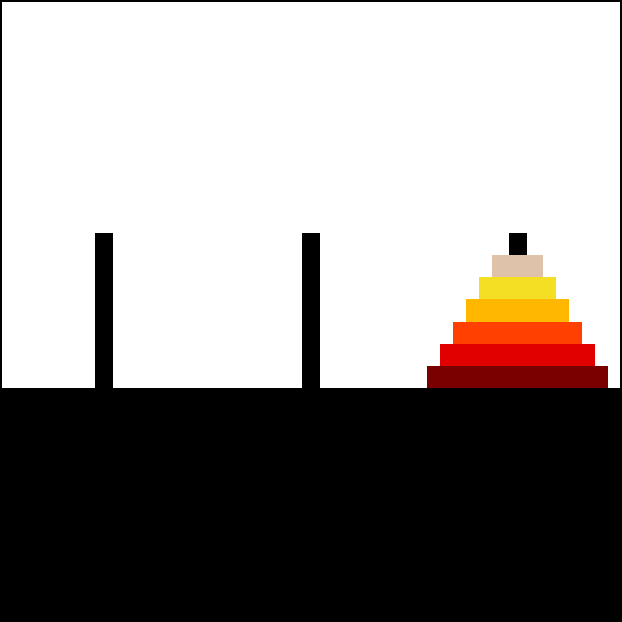作业 3:递归、树形递归 hw03.zip¶
下载 hw03.zip
MOLI:本次作业你将会学到什么
- 基础递归:锻炼大家真正理解递归控制流的本质:每一次函数调用都在解决一个更小规模的同类问题
- 互斥递归与辅助函数:通过定义内部辅助函数或互相调用的递归,掌握“交替执行”与“状态传递”技巧
- 树形递归:递归的结果会产生一棵递归树,锻炼大家完整枚举这棵树所有解
- 无状态与有状态递归:锻炼大家在复杂场景下,在递归中记录每个状态
- 问题抽象与分解:学会如何用递归,来解“组合计数”类问题,并推广到其他问题
必答题¶
Q1:数字8的个数¶
编写一个递归函数 num_eights ,它接受一个正整数 n ,并返回数字 n 中8出现的次数。
注意:必须使用递归;如果使用任何赋值语句或循环,测试将失败。(你可以定义新的函数,但那里也不要使用赋值语句。)
def num_eights(n):
"""返回数字n中8出现的次数。
>>> num_eights(3)
0
>>> num_eights(8)
1
>>> num_eights(88888888)
8
>>> num_eights(2638)
1
>>> num_eights(86380)
2
>>> num_eights(12345)
0
>>> num_eights(8782089)
3
>>> from construct_check import check
>>> # 禁止所有的赋值语句
>>> check(HW_SOURCE_FILE, 'num_eights',
... ['Assign', 'AnnAssign', 'AugAssign', 'NamedExpr', 'For', 'While'])
True
"""
"*** 在这里填写你的代码 ***"使用ok来测试你的代码:
python3 ok -q num_eights --localQ2:数字距离¶
对于一个给定的整数,数字距离指的是连续数字对之差的绝对值之和。例如:
61的数字距离是5,因为6 - 1的绝对值是5。71253的数字距离是12(abs(7-1) + abs(1-2) + abs(2-5) + abs(5-3)=6 + 1 + 3 + 2)。6的数字距离是0,因为没有连续的数字对。
编写一个函数来确定正整数的数字距离。你必须使用递归,否则测试将失败。
def digit_distance(n):
"""确定正整数的数字距离
>>> digit_distance(3)
0
>>> digit_distance(777) # 0 + 0
0
>>> digit_distance(314) # 2 + 3
5
>>> digit_distance(31415926535) # 2 + 3 + 3 + 4 + ... + 2
32
>>> digit_distance(3464660003) # 1 + 2 + 2 + 2 + ... + 3
16
>>> from construct_check import check
>>> # 禁止所有的循环
>>> check(HW_SOURCE_FILE, 'digit_distance',
... ['For', 'While'])
True
"""
"*** 在这里填写你的代码 ***"使用ok来测试你的代码:
python3 ok -q digit_distance --localQ3:交错和¶
编写函数 interleaved_sum,该函数接收一个数字 n 和两个单参数函数:odd_func 与 even_func。函数返回的结果是:将 odd_func 应用到 1 到 n(包括 n)的所有奇数,并将 even_func 应用到所有偶数,最后将这些结果相加的总和。
例如,执行 interleaved_sum(5, lambda x: x, lambda x: x * x) 会返回 1 + 2*2 + 3 + 4*4 + 5 = 29 。
重要提示:实现此函数时,不得使用任何循环,也不可直接判断数字的奇偶性(例如禁止使用
%运算符)。相反,应从已知的奇数1开始,通过交替计算奇数和偶数的方式实现。提示:可以引入一个内部辅助函数,该函数接收一个奇数
k,并计算从k到n(闭区间)的交错和。或者,你也可以使用相互递归来实现。
def interleaved_sum(n, odd_func, even_func):
"""计算odd_func(1) + even_func(2) + odd_func(3) + ...,直到n的总和.
>>> identity = lambda x: x
>>> square = lambda x: x * x
>>> triple = lambda x: x * 3
>>> interleaved_sum(5, identity, square) # 1 + 2*2 + 3 + 4*4 + 5
29
>>> interleaved_sum(5, square, identity) # 1*1 + 2 + 3*3 + 4 + 5*5
41
>>> interleaved_sum(4, triple, square) # 1*3 + 2*2 + 3*3 + 4*4
32
>>> interleaved_sum(4, square, triple) # 1*1 + 2*3 + 3*3 + 4*3
28
>>> from construct_check import check
>>> check(HW_SOURCE_FILE, 'interleaved_sum', ['While', 'For', 'Mod']) # 禁用循环和%
True
>>> check(HW_SOURCE_FILE, 'interleaved_sum', ['BitAnd', 'BitOr', 'BitXor']) # 禁用位运算符(如果不了解这是什么,也不用担心)
True
"""
"*** 在这里填写你的代码 ***"使用ok来测试你的代码:
python3 ok -q interleaved_sum --localQ4: 计算美元¶
对于给定的正整数总额(total),若一组美元纸币的面值之和等于该总额,则称这组纸币可以组成该总额的找零。这里我们使用标准美元纸币面额:1、5、10、20、50和100。例如,以下各组纸币都可以组成 15 美元的找零:
- 15张1美元的钞票
- 10张1美元的钞票,1张5美元的钞票
- 5张1美元的钞票,2张5美元的钞票
- 5张1美元,1张10美元钞票
- 3张5美元钞票
- 1张5美元,1张10美元钞票
因此,共有6种方法可以凑出 15 美元的找零。请编写一个**递归函数** count_dollars ,该函数接收一个正整数 total 作为参数,返回使用1、5、10、20、50和100美元纸币凑出该总额的所有可能方式的数量。
请在您的解决方案中使用 next_smaller_dollar 函数:该函数将返回比输入面值更小的下一个标准美元纸币面额(例如,next_smaller_dollar(5) 将返回 1)。若不存在更小面额的纸币,则函数返回 None。
重要提示:请使用递归实现,若使用循环将导致测试失败。 提示:可参考
count_partitions的实现示例,了解如何通过逐步累加较小数值来统计总和达到目标值。若需要在函数递归调用之间追踪多个值,建议编写辅助函数。
def next_smaller_dollar(bill):
"""返回比输入面值更小的下一个美元面额"""
if bill == 100:
return 50
if bill == 50:
return 20
if bill == 20:
return 10
elif bill == 10:
return 5
elif bill == 5:
return 1
def count_dollars(total):
"""返回凑出该总额的所有可能方式的数量
>>> count_dollars(15) # 15 $1 bills, 10 $1 & 1 $5 bills, ... 1 $5 & 1 $10 bills
6
>>> count_dollars(10) # 10 $1 bills, 5 $1 & 1 $5 bills, 2 $5 bills, 10 $1 bills
4
>>> count_dollars(20) # 20 $1 bills, 15 $1 & $5 bills, ... 1 $20 bill
10
>>> count_dollars(45) # 有多少种方式凑出45美元?
44
>>> count_dollars(100) # 有多少种方式凑出100美元?
344
>>> count_dollars(200) # 有多少种方式凑出200美元?
3274
>>> from construct_check import check
>>> # 禁用迭代
>>> check(HW_SOURCE_FILE, 'count_dollars', ['While', 'For'])
True
"""
"*** 在这里填写你的代码 ***" 使用ok来测试你的代码:
python3 ok -q count_dollars --local检查你的得分¶
运行得到本次作业中每个问题的分数。
python3 ok --score --local可选问题¶
这些问题可自行选做。即使不完成也不会影响作业的得分。但它们是非常好的练习材料,建议还是认真完成!
Q5: 升序统计美元金额¶
编写**递归函数** count_dollars_upward,其功能与 count_dollars 相同,但改用 next_larger_dollar 函数——该函数会返回比输入面值更大的下一个标准美元纸币面额(例如 next_larger_dollar(5) 返回 10)。若不存在更大面额的纸币,则返回 None。
重要提示:必须使用递归实现,使用循环将无法通过测试。
def next_larger_dollar(bill):
"""返回比输入面值更大的下一个美元面额"""
if bill == 1:
return 5
elif bill == 5:
return 10
elif bill == 10:
return 20
elif bill == 20:
return 50
elif bill == 50:
return 100
def count_dollars_upward(total):
"""返回凑出该总额的所有可能方式的数量
>>> count_dollars_upward(15) # 15 $1 bills, 10 $1 & 1 $5 bills, ... 1 $5 & 1 $10 bills
6
>>> count_dollars_upward(10) # 10 $1 bills, 5 $1 & 1 $5 bills, 2 $5 bills, 10 $1 bills
4
>>> count_dollars_upward(20) # 20 $1 bills, 15 $1 & $5 bills, ... 1 $20 bill
10
>>> count_dollars_upward(45) # 有多少种方式凑出45美元?
44
>>> count_dollars_upward(100) # 有多少种方式凑出100美元?
344
>>> count_dollars_upward(200) # 有多少种方式凑出200美元?
3274
>>> from construct_check import check
>>> # 禁用迭代
>>> check(HW_SOURCE_FILE, 'count_dollars_upward', ['While', 'For'])
True
"""
"*** 在这里填写你的代码 ***"使用ok来测试你的代码:
python3 ok -q count_dollars_upward --local考试练习¶
作业也会包含之前的考试级别问题供你参考。这些问题不需要提交;如果你喜欢挑战,那就可以尝试它们!
- 2017 年秋季 MT1 Q4a:数字
- 2019 年秋季期末考试 Q6b:回文
仅供娱乐的问题¶
以下问题不在61A课程范围内。如果你想挑战自我可以尝试,但这些题目只是趣味谜题,并非课程要求。绝大多数学生都会跳过这些问题,这完全没有问题。我们不会在Ed平台或答疑时间优先支持这些问题的解答。
Q6:汉诺塔¶
汉诺塔(Towers of Hanoi)是一个经典益智游戏,由三根杆和若干大小不一的圆盘组成,这些圆盘可套入任意杆上。游戏初始时,所有 n 个圆盘按大小升序排列在起始杆 start 上,最小的盘位于顶端,整体形成一个圆锥形结构。

该谜题的目标是将整个塔盘移动到目标杆 end 上,且需遵循以下规则:
- 每次只能移动一个盘片
- 每次移动需取走某根杆最顶部(最小)的盘片,将其滑到另一根杆上,可置于该杆现有盘片之上
- 任何盘片都不能放置在比它小的盘片上方
请补全 move_stack 函数的定义,该函数需打印出将 n 个盘片从起始杆 start 移动到目标杆 end 且不违反规则的步骤。已提供的 print_move 函数会打印出单个盘片从起始杆移动到目标杆的具体步骤。
提示:在纸上绘制出不同
n值时的游戏过程,尝试找出适用于任意n值的圆盘移动规律。在解决方案中,当需要移动少于n个圆盘时,可直接采用递归思维进行处理。如需更多帮助,请参考以下提示。
提示 2
汉诺塔问题的解决策略是:首先将除最底层圆盘外的所有圆盘移至第二根杆,接着将最底层圆盘移至第三根杆,最后将第二根杆上除底层外的所有圆盘移至第三根杆。
提示 3
你无需担心怎么去收集所有步骤。只要你确保移动步骤是按顺序打印的,print 就能有效地在终端中"收集"所有结果。
def print_move(origin, destination):
"""打印移动盘片的指令"""
print("Move the top disk from rod", origin, "to rod", destination)
def move_stack(n, start, end):
"""打印将 n 个圆盘从起始杆移动到目标杆所需的步骤,且不违反汉诺塔规则。
n -- 圆盘数量
start -- 起始杆位置(取值为 1、2 或 3)
end -- 目标杆位置(取值为 1、2 或 3)
共有三根柱子,且起始柱和目标柱必须不同。假设起始柱上至少有n个尺寸递增的圆盘,而目标柱要么为空,要么其顶部圆盘的尺寸大于起始柱顶部n个圆盘的尺寸。
>>> move_stack(1, 1, 3)
Move the top disk from rod 1 to rod 3
>>> move_stack(2, 1, 3)
Move the top disk from rod 1 to rod 2
Move the top disk from rod 1 to rod 3
Move the top disk from rod 2 to rod 3
>>> move_stack(3, 1, 3)
Move the top disk from rod 1 to rod 3
Move the top disk from rod 1 to rod 2
Move the top disk from rod 3 to rod 2
Move the top disk from rod 1 to rod 3
Move the top disk from rod 2 to rod 1
Move the top disk from rod 2 to rod 3
Move the top disk from rod 1 to rod 3
"""
assert 1 <= start <= 3 and 1 <= end <= 3 and start != end, "Bad start/end"
"*** 在这里填写你的代码 ***"使用ok来测试你的代码:
python3 ok -q move_stack --localQ7: 匿名阶乘¶
在不为递归函数分配全局框架名称的情况下,这个问题展示了我们仍然可以编写递归函数。
通过使用条件表达式,递归阶乘函数可以写成一个单一的表达式。
>>> fact = lambda n: 1 if n == 1 else mul(n, fact(sub(n, 1)))
>>> fact(5)
120然而,这种实现方式依赖于一个事实,即 fact 必须有一个名字(这里不是双关语),然后我们才能在函数体内引用它。以往编写递归函数时,我们总是通过 def 或赋值语句为其命名,以便在函数体内引用自身。而在这个问题中,你的任务是在不给函数命名的情况下,递归地定义 fact!
写一个表达式,它只能通过使用调用表达式、条件表达式和 lambda 表达式(不使用赋值或 def 语句)来计算 n 的阶乘。
注意:在返回的表达式中,不允许使用
make_anonymous_factorial。
要解决这个问题, operator 模块中的 sub 和 mul 函数是你唯一需要使用的内置函数。
from operator import sub, mul
def make_anonymous_factorial():
"""返回计算阶乘的表达式的值
>>> make_anonymous_factorial()(5)
120
>>> from construct_check import check
>>> # 禁用任何赋值和递归
>>> check(HW_SOURCE_FILE, 'make_anonymous_factorial',
... ['Assign', 'AnnAssign', 'AugAssign', 'NamedExpr', 'FunctionDef', 'Recursion'])
True
"""
return '在这里编写你的表达式'使用ok来测试你的代码:
python3 ok -q make_anonymous_factorial --local